1:53 AM Ball Rolling on Tilted Turntable | |
Ball Rolling on Tilted TurntableMichael Fowler IntroductionWe'll now consider an interesting dynamics problem not covered in most introductory texts, a rolling ball on a rotating, possibly tilted, surface. As we'll see, this tough-sounding problem is not that difficult to solve using Newtonian methods, and leads to some surprising results. For example, a ball rolling on a steadily rotating horizontal plane moves in a circle, and not a circle centered at the axis of rotation. We'll prove this -- and demonstrate it in class. Even more remarkably, if the rotating plane is tilted, the ball follows a cycloidal path, keeping at the same average height -- not rolling downhill. (This is exactly analogous to an electron in crossed electric and magnetic fields!) One reason the rolling ball problems are generally avoided is that they do not readily lend themselves to a Lagrangian analysis, but can in fact be solved quite quickly with a vectorized application of Newton's laws. The appropriate techniques are described in Milne's book Vectorial Mechanics, which we follow. Holonomic Constraints and non-Holonomic ConstraintsA spherical ball rolling on a plane without slipping is constrained in its translational and rotational motion by the requirement that the point of the sphere momentarily in contact with the plane is at rest. How do we incorporate this condition in the dynamical analysis: the least action approach, for example, or the direct Newtonian equations of motion?
A constraint on a dynamical system that can be integrated in this way to eliminate one of the variables is called a holonomic constraint. A constraint that cannot be integrated is called a nonholonomic constraint. For a sphere rolling on a rough plane, the no-slip constraint turns out to be nonholonomic. To see this, imagine a sphere placed at the origin in the Now start again at the origin, the N pole on top. This time, first roll the sphere through ninety degrees in the The bottom line is that, in contrast to the cylindrical case, for a rolling sphere the no-slip constraint does not allow us to eliminate any dynamical variables -- given that initially the sphere is at the origin with the N pole at the top, there is no unique relationship between orientation So the constraint equation, which can be written
does not allow us to eliminate a variable, but it certainly plays a role in the dynamics! As we've seen, the identical equation for the cylinder
trivially integrates to A possible approach is to use Lagrange multipliers to take account of the constraint, just as in deriving the equation for the catenary the fixed length of the string entered as a constraint. Doing this for the rolling ball turns out to lead to a very messy problem -- for once, the advanced approach to dynamics doesn't pay off. But there's a better way. D'Alembert's PrincipleThe "better way" is simply to write down Newton's equations, Footnote: We're not going to pursue this here, but the "principle" stems from the concept of virtual work: if a system is in equilibrium, then making tiny displacements of all parameters, subject to the system constraints (but not necessarily an infinitesimal set of displacements that would arise in ordinary dynamical development in time), the total work done by all forces acting on parts of the system is zero. This is just saying that in equilibrium, it is at a local minimum (or stationary point if we allow unstable equilibrium) in the energy "landscape". D'Alembert generalized this to the dynamical case by adding in effective forces corresponding to the coordinate accelerations, he wrote essentially Having written down the equations, the reaction forces can be cancelled out to derive equations of motion. Ball with External Forces Rolling on Horizontal PlaneHere's how it works for a simple example (done in Landau, and see diagram below): the equation of motion of a sphere rolling on a fixed horizontal plane under an external force Taking the reaction at the plane to be
The constraint equation, differentiated, gives substituting
This equation gives the components of the reaction force as functions of the external force and couple: the velocities have been eliminated. So we can now put
and substitution in the original equations of motion gives
Exercise: interpret this for the zero torque case, and for the zero force case. Landau goes on to solve three statics problems (meaning simple use of d'Alembert's principle) which could be in an introductory physics course. We'll skip them. Ball Rolling on a Rotating Turntable(The following examples are from Milne, Vectorial Mechanics.) A sphere is rolling without slipping on a horizontal plane. The plane is itself rotating (about a fixed vertical axis) at constant angular velocity Problem: Find the path of the center of the sphere We have three vector equations: Newton's equations for linear and angular acceleration, and the rolling condition. We'll use them to eliminate two (vector) variables we don't need: the reaction force between the plane and the ball The equations of motion of the sphere (radius
(Of course, the gravitational force here is just balancing the vertical component of the reaction force. This will no longer be the case for the tilted plane, treated in the next section.) First, we'll eliminate the reaction force
The rolling condition is:
the right-hand side being the local velocity of the turntable, We'll use the rolling condition to eliminate First, differentiate it (remember
Next, take the equation of motion
and putting these together to get rid of the angular velocity,
This integrates to
which is just the equation for steady circular motion about the point For a uniform sphere, So the ball rolling on the rotating plate goes around in a circle, which could be any circle. If it is put down gently at any point on the rotating plane, and held in place until it is up to speed (meaning no slipping) it will stay at that point for quite a while (until the less than perfect conditions, such as air resistance or vibration, cause noticeable drift). If it is nudged, it will move in a circle. In class, we saw it circle many times -- eventually, it fell off, a result of air resistance plus the shortcomings of our apparatus, but the circular path was very clear. Ball Rolling on a Tilted Rotating Plane
The equations of motion are:
and the equation of rolling contact is First, we eliminate
Note that Integrating,
Now eliminate
then using
The constant is fixed by the initial position
The first term in the square brackets would give the same circular motion we found for the horizontal rotating plane, the second term adds a steady motion of the center of this circle, in a horizontal direction (not down the plane!) at constant speed (This is identical to the motion of a charged particle in crossed electric and magnetic fields. You should check, by differentiating the above equation, and proving you get the charged particle result.) Bottom line: the intuitive notion that a ball rolling on a rotating inclined turntable would tend to roll downhill is wrong. Recall that for a particle circling in a magnetic field, if an electric field is added perpendicular to the magnetic field, the particle moves in a cycloid at the same average electrical potential -- it has no net movement in the direction of the electric field, only perpendicular to it. Our rolling ball follows an identical cycloidal path -- keeping the same average gravitational potential. Exercise: convince yourself that the rotation generates a term in the equation of motion exactly equivalent to the magnetic force term for a moving charged particle. Note that both these terms are not time-reversal invariant. | |
|
| |
| Total comments: 37 | 1 2 3 ... 7 8 » | |||||
| ||||||
| 1-5 6-10 11-15 ... 31-35 36-37 | ||||||
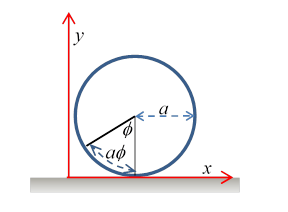 We'll begin with a simpler example, that of a cylinder, rolling in the
We'll begin with a simpler example, that of a cylinder, rolling in the
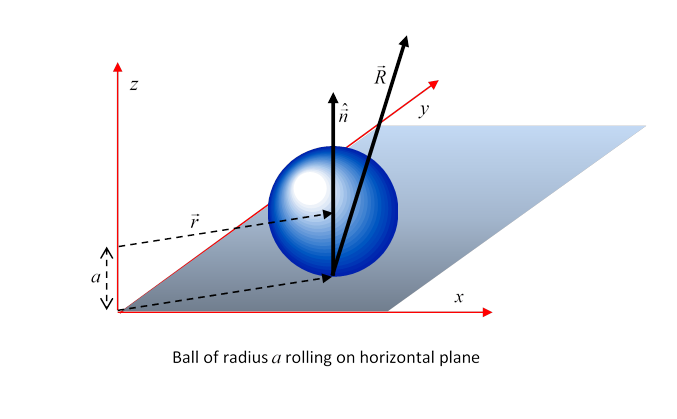


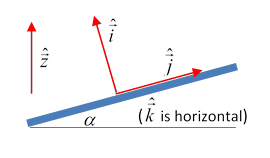 We'll take unit vectors
We'll take unit vectors 

 we find
we find