1:08 AM A New Way to Write the Action Integral | |
A New Way to Write the Action IntegralIntroductionFollowing Landau, we'll first find how the action integral responds to incremental changes in the endpoint coordinates and times, then use the result to write the action integral itself in a new, more intuitive way. This new formulation shows very directly the link to quantum mechanics, and variation of the action in this form gives Hamilton's equations immediately. Function of Endpoint Position
Taking one degree of freedom (the generalization is straightforward), for a small path variation the incremental change in action
(Recall that first term comes from the calculus of variations when we allow the end point to vary -- it's exactly the same point we previously discussed in the brachistochrone problem of fastest time for a given horizontal distance, allowing the vertical position of the endpoint to be a free parameter.) With the incremental variation, we've gone from the physical path Both paths Writing
For the multidimensional case, the incremental change in the action on varying the final position variable is given by (dropping the superscript)
Function of Endpoint TimeWhat about the action as a function of the final point arrival time? Since Remember we are defining the action at a point as that from integrating along the true path up to that point. Landau denotes If we now allow an incremental time increase, This will give (with
Putting this together with
and therefore, combining this with the result
This, then, is the total differential of the action as a function of the spatial and time coordinates of the end of the path. Varying Both EndsThe argument given above for the incremental change in action from varying the endpoint is clearly equally valid for varying the beginning point of the integral (there will be a sign change, of course), so
The initial and final coordinates and times specify the action and the time development of the system uniquely. (Note: We'll find this equation again in the section on canonical transformations -- the action will be seen there to be the generating function of the time-development canonical transformation, this will become clear when we get to it.) Another Way of Writing the Action IntegralUp to this point, we've always written the action as an integral of the Lagrangian with respect to time along the path,
However, the expression derived in the last section for the increment of action generated by an incremental change in the path endpoint is clearly equally valid for the contribution to the action from some interior increment of the path, say from
In this integral, of course, the (In writing How this Classical Action Relates to Phase in Quantum MechanicsThe link between classical and quantum mechanics is particularly evident in the expression for the action integral given above. In the so-called semi-classical regime of quantum mechanics, the de Broglie waves oscillate with wavelengths much smaller than typical sizes in the system. This means that locally it's an adequate approximation to treat the Schrodinger wave function as a plane wave,
where the amplitude function As we've discussed earlier, in the Dirac-Feynman formulation of quantum mechanics, to find the probability amplitude of a particle propagating from one point to another, we add contributions from all possible paths between the two points, each path contributing a term with phase equal to From the semi-classical Schrodinger wave function above, it's clear that the change in phase from a small change in the endpoint is
So again we see, here very directly, how the action along a classical path is a multiple of the quantum mechanical phase change along the path. Hamilton's Equations from Action MinimizationFor arbitrary small path variations (Note for nitpickers: This may seem a bit surprising, since we generated this form of the action using the equations along the actual dynamical path, how can we vary it and still use them? Bear with me, you'll see.) We'll prove this for a one dimensional system, it's trivial to go to many variables, but it clutters up the equations. For a small path deviation
and integrating
The path variations Again, it's worth emphasizing the close parallel with quantum mechanics: Hamilton's equations written using Poisson brackets are:
In quantum mechanics, the corresponding Heisenberg equations of motion for position and momentum operators in terms of commutators are
How Can p, q Really Be Independent Variables?It may seem a little odd at first that varying The answer is, no, This comes about as follows: Along the minimum action path, we just established that
We also have that
from which, along the physical path, | |
|
| |
| Total comments: 0 | |
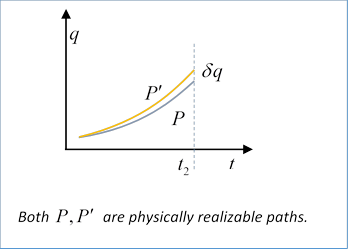 We'll now think of varying the action in a slightly different way. (Note: We're using Landau's notation.) Previously, we considered the integral of the Lagrangian over all possible different paths from the initial place and time
We'll now think of varying the action in a slightly different way. (Note: We're using Landau's notation.) Previously, we considered the integral of the Lagrangian over all possible different paths from the initial place and time 
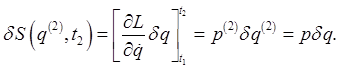
 the total time derivative
the total time derivative 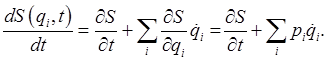
 .
.
