Ball Rolling on Tilted Turntable
Michael Fowler
Introduction
We'll now consider an interesting dynamics problem not covered in most introductory texts, a rolling ball on a rotating, possibly tilted, surface. As we'll see, this tough-sounding problem is not that difficult to solve using Newtonian methods, and leads to some surprising results. For example, a ball rolling on a steadily rotating horizontal plane moves in a circle, and not a circle centered at the axis of rotation. We'll prove this -- and demonstrate it in class. Even more remarkably, if the rotating plane is tilted, the ball follows a cycloidal path, keeping at the same average height -- not rolling downhill. (This is exactly analogous to an electron in crossed electric and magnetic fields!) One reason the rolling ball problems are generally avoided is that they do not readily lend themselves to a Lagrangian analysis, but can in fact be solved quite quickly with a vectorized application of Newton's laws. The appropriate techniques are described in Milne's book Vectorial Mechanics, which we follow.
Holonomic Constraints and non-Holonomic Constraints
A spherical ball rolling on a plane without slipping is constrained in its translational and rotational motion by the requirement that the point of the sphere momentarily in contact with the plane is at rest. How do we incorporate this conditi
...
Read more »
|
Euler's Equations
Michael Fowler
Introduction
We've just seen that by specifying the rotational direction and the angular phase of a rotating body using Euler's angles, we can write the Lagrangian in terms of those angles and their derivatives, and then derive equations of motion. These can be solved to describe precession, nutation, etc.
One might hope for a more direct Newtonian approach -- we know, for example, that the steadily precessing child's top is easy to understand in terms of the gravitational torque rotating the angular momentum vector. What about applying 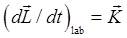 (the external torque on the system) more generally? It's certainly valid. The problem is that in the lab frame (the external torque on the system) more generally? It's certainly valid. The problem is that in the lab frame 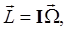 meaning meaning 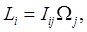 and the elements of the inertia tensor relative to the lab axes are constantly changing as the body rotates. The Newtonian approach is only practicable if the connection between and the elements of the inertia tensor relative to the lab axes are constantly changing as the body rotates. The Newtonian approach is only practicable if the connection between 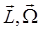 can be made in the body frame defined by
...
Read more » can be made in the body frame defined by
...
Read more »
|
Euler's Angles
Michael Fowler
Introduction
So far, our analysis of rotational motion has been of essentially one dimensional, or more precisely one angular parameter, motion: rotating about an axis, rolling, precessing, etc. But this leaves out many interesting phenomena: the wobbling of a slowing down top, nutation, and so on. We need a well-defined set of parameters for the orientation of a rigid body in space to make further progress in analyzing the dynamics.
The standard set is Euler's Angles. What you actually observe as you watch a child's top beginning to wobble as it slows down is the changing direction of the axis -- this direction is given by the first two of Euler's angles: 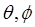 which are just the usual spherical coordinates, the angle which are just the usual spherical coordinates, the angle 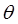 measured from the vertical direction and the azimuthal angle measured from the vertical direction and the azimuthal angle 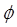 about that vertical axis. Euler's third angle, about that vertical axis. Euler's third angle,  specifies the orientation of the top about its own axis, completing the description of th
...
Read more » specifies the orientation of the top about its own axis, completing the description of th
...
Read more »
|
Rigid Body Moving Freely
Michael Fowler
Angular Momentum and Angular Velocity
In contrast to angular velocity, the angular momentum of a body depends on the point with respect to which it is defined. For now, we take it (following Landau, of course) as relative to the center of mass, but we denote it by 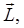 following modern usage. This "intrinsic" angular momentum is like the Earth's angular momentum from its diurnal rotation, as distinct from its orbital angular momentum in going around the Sun. following modern usage. This "intrinsic" angular momentum is like the Earth's angular momentum from its diurnal rotation, as distinct from its orbital angular momentum in going around the Sun.
That is,
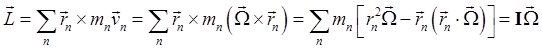
where 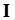 is the inertia tensor: this just means is the inertia tensor: this just means 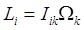 . .
Explicitly, taking the principal axes as the 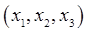 axes, axes,
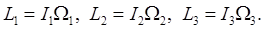
For anything with spherical inertial symmetry
...
Read more »
|
Motion of a Rigid Body: the Inertia Tensor
Michael Fowler
Definition of Rigid
We're thinking here of an idealized solid, in which the distance between any two internal points stays the same as the body moves around. That is, we ignore vibrations, or strains in the material resulting from inside or outside stresses. In fact, this is almost always an excellent approximation for ordinary solids subject to typical stresses -- obvious exceptions being rubber, flesh, etc. Following Landau, we'll usually begin by representing the body as a collection of particles of different masses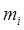 held in their places held in their places 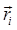 by massless bonds. This approach has the merit that the dynamics can be expressed cleanly in terms of sums over the particles, but for an ordinary solid we'll finally take a continuum limit, replacing the finite sums over the constituent particles by integrals over a continuous mass distribution. by massless bonds. This approach has the merit that the dynamics can be expressed cleanly in terms of sums over the particles, but for an ordinary solid we'll finally take a continuum limit, replacing the finite sums over the constituent particles by integrals over a continuous mass distribution.
Rotation of a Body about a Fixed Axis
 As a preliminary, let's look at a body firmly attached to a rod fixed in space, and rotating with angular veloci
...
Read more » As a preliminary, let's look at a body firmly attached to a rod fixed in space, and rotating with angular veloci
...
Read more »
|
Anharmonic Oscillators
Michael Fowler
Introduction
Landau (para 28) considers a simple harmonic oscillator with added small potential energy terms 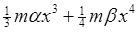 . We'll simplify slightly by dropping the . We'll simplify slightly by dropping the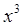 term, to give an equation of motion term, to give an equation of motion
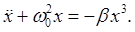
(We'll always take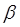 positive, otherwise only small oscillations will be stable.) positive, otherwise only small oscillations will be stable.)
We'll do perturbation theory (following Landau):
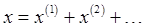
(Standard practice in most books would be to write 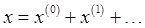 with the superscript indicating the order of the perturbation -- we're following Landau's notation, hopefully reducing confusion...) with the superscript indicating the order of the perturbation -- we're following Landau's notation, hopefully reducing confusion...)
We take as the leading term
 ...
Read more »
...
Read more »
|
Motion in a Rapidly Oscillating Field: the Ponderomotive Force
Michael Fowler
Introduction
Imagine first a particle of mass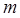 moving along a line in a smoothly varying potential moving along a line in a smoothly varying potential 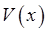 , so , so 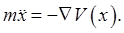 Now add in a rapidly oscillating force, not necessarily small, acting on the particle: Now add in a rapidly oscillating force, not necessarily small, acting on the particle:
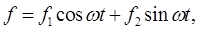
where 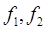 are in general functions of position. This force is oscillating much more rapidly than any oscillation of the particle in the original potential, and we'll assume that the position of the particle as a function of time can be written as a sum of a "slow motion" are in general functions of position. This force is oscillating much more rapidly than any oscillation of the particle in the original potential, and we'll assume that the position of the particle as a function of time can be written as a sum of a "slow motion" 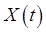 and a rapid oscillation and a rapid oscillation 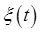 , ,
...
Read more »
|
Parametric Resonance
Michael Fowler
Introduction
(Following Landau para 27)
A one-dimensional simple harmonic oscillator, a mass on a spring,
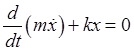
has two parameters, 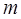 and and 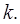 For some systems, the parameters can be changed externally (an example being the length of a pendulum if at the top end the string goes over a pulley). For some systems, the parameters can be changed externally (an example being the length of a pendulum if at the top end the string goes over a pulley).
We are interested here in the system's response to some externally imposed periodic variation of its parameters, and in particular we'll be looking at resonant response, meaning large response to a small imposed variation.
Note first that imposed variation in the mass term is easily dealt with, by simply redefining the time variable to 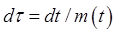 , meaning , meaning 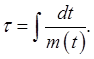
Then
 ...
Read more »
...
Read more »
|
Dynamics of a One-Dimensional Crystal
Michael Fowler
The Model
Notation! In this lecture, I use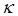 for the spring constant ( for the spring constant (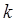 is a wave number) and is a wave number) and 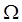 for frequency ( for frequency (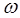 is a root of unity). is a root of unity).
A good classical model for a crystal is to represent the atoms by balls held in place by light springs, representing valence bonds, between nearest neighbors. The simplest such crystal that has some realistic features is a single chain of connected identical atoms. To make the math easy, we'll connect the ends of the chain to make it a circle. This is called "imposing periodic boundary conditions". It is common practice in condensed matter theory, and makes little difference to the physics for a large system.
We'll take the rest positions of the atoms to be uniformly spaced, 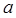 apart, with the first atom at apart, with the first atom at  ...
Read more »
...
Read more »
|
Driven Oscillator
Michael Fowler (closely following Landau para 22)
Consider a one-dimensional simple harmonic oscillator with a variable external force acting, so the equation of motion is
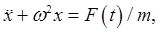
which would come from the Lagrangian
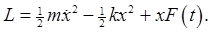
(Landau "derives" this as the leading order non-constant term in a time-dependent external potential.)
The general solution of the differential equation is 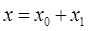 , where , where 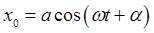 , the solution of the homogeneous equation, and , the solution of the homogeneous equation, and 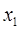 is some particular integral of the inhomogeneous equation. is some particular integral of the inhomogeneous equation.
An important case is that of a periodic driving force 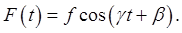 A trial solution A trial solution  ...
Read more »
...
Read more »
|
Elastic Scattering
Michael Fowler
Billiard Balls
"Elastic" means no internal energy modes of the scatterer or of the scatteree are excited -- so total kinetic energy is conserved. As a simple first exercise, think of two billiard balls colliding. The best way to see it is in the center of mass frame of reference. If they're equal mass, they come in from opposite directions, scatter, then move off in opposite directions. In the early days of particle accelerators (before colliders) a beam of particles was directed at a stationary target. So, the frame in which one particle is initially at rest is called the lab frame. What happens if we shoot one billiard ball at another which is initially at rest? (We'll ignore possible internal energies, including spinning.) The answer is that they come off at right angles. This follows trivially from conservation of energy and momentum (in an obvious notation)
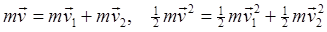
and Pythagoras' theorem.
Discovery of the Nucleus
The first significant use of scattering to learn about the internal structure of matter was Rutherford's use of  ...
Read more »
...
Read more »
|
A Vectorial Approach: Hamilton's Equation and the Runge Lenz Vector
(Mainly following Milne, Vectorial Mechanics, p 235 on.)
Laplace and Hamilton developed a rather different approach to this inverse-square orbit problem, best expressed vectorially, and made a surprising discovery: even though conservation of angular momentum and of energy were enough to determine the motion completely, for the special case of an inverse-square central force, something else was conserved. So the system has another symmetry!
Hamilton's approach (actually vectorized by Gibbs) was to apply the operator 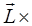 ...
Read more »
...
Read more »
|
Dynamics of Motion in a Central Potential: Deriving Kepler's Laws
Conserved Quantities
The equation of motion is:
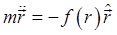 .
...
Read more » .
...
Read more »
|
Adiabatic Invariants and Action-Angle Variables
Michael Fowler
Adiabatic Invariants
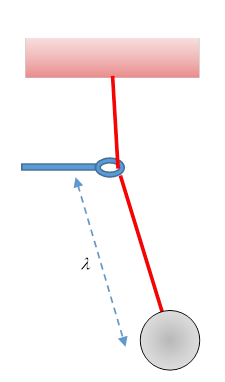 Imagine a particle in one dimension oscillating back and forth in some potential. The potential doesn't have to be harmonic, but it must be such as to trap the particle, which is executing periodic motion with period Imagine a particle in one dimension oscillating back and forth in some potential. The potential doesn't have to be harmonic, but it must be such as to trap the particle, which is executing periodic motion with period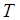 . Now suppose we gradually change the potential, but keeping the particle trapped. That is, the potential depends on some parameter . Now suppose we gradually change the potential, but keeping the particle trapped. That is, the potential depends on some parameter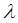 , which we change gradually, meaning over a time much greater than the time of oscillation: , which we change gradually, meaning over a time much greater than the time of oscillation: 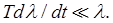
A crude demonstration is a simple pendulum with a string of variable length, for example (see figure) one hanging from a fixed support, but the string passing through a small loop that can be moved vertically to change the effective length.
If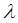 were fixed, the system would have constant energy were fixed, the system would have constant energy ![]() ...
Read more »
...
Read more »
|
The Hamilton-Jacobi Equation
Michael Fowler
Back to Configuration Space
We've established that the action, regarded as a function of its coordinate endpoints and time, satisfies
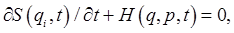
and at the same time 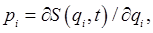 so so 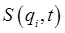 obeys the first-order differential equation obeys the first-order differential equation
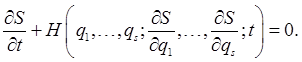
This is the Hamilton-Jacobi equation.
Notice that we're now back in configuration space!
For example, the Hamilton-Jacobi equation for the simple harmonic oscillator in one dimension is
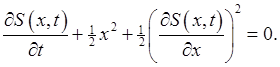
(Notice that this has some resemblance to the Schrödinger equation for the same system.)
If the Hamiltonian has no explicit time dependence 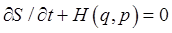 becomes just becomes just ![]() ...
Read more »
...
Read more »
|
Introduction to Liouville's Theorem
Paths in Simple Phase Spaces: the SHO and Falling Bodies
Let's first think further about paths in phase space. For example, the simple harmonic oscillator, with Hamiltonian 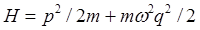 , describes circles in phase space parameterized with the variables , describes circles in phase space parameterized with the variables 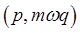 . (A more usual notation is to write the potential term as . (A more usual notation is to write the potential term as 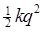 .) .)
Question: are these circles the only possible paths for the oscillator to follow?
Answer: yes: any other path would intersect a circle, and at that point, with both position and velocity defined, there is only one path forward (and back) in time possible, so the intersection can't happen.
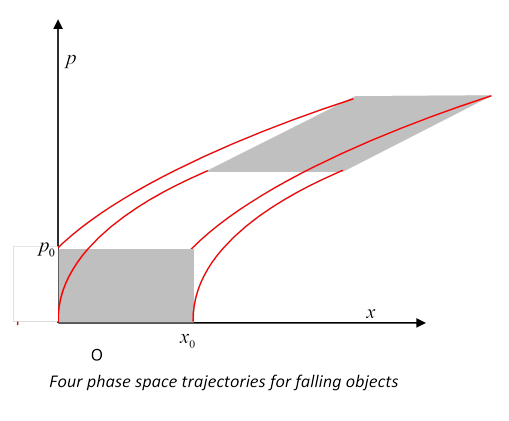 Here's an example from Taylor of paths in phase space: four identical falling bodies are released simultaneously, see figure, Here's an example from Taylor of paths in phase space: four identical falling bodies are released simultaneously, see figure, 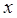 measures distance vertically down. Tw
...
Read more » measures distance vertically down. Tw
...
Read more »
|
Canonical Transformations
Point Transformations
It's clear that Lagrange's equations are correct for any reasonable choice of parameters labeling the system configuration. Let's call our first choice 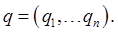 Now transform to a new set, maybe even time dependent, Now transform to a new set, maybe even time dependent, 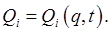 The derivation of Lagrange's equations by minimizing the action still works, so Hamilton's equations must still also be OK too. This is called a point transformation: we've just moved to a different coordinate system, we're relabeling the points in configuration space (but possibly in a time-dependent way). The derivation of Lagrange's equations by minimizing the action still works, so Hamilton's equations must still also be OK too. This is called a point transformation: we've just moved to a different coordinate system, we're relabeling the points in configuration space (but possibly in a time-dependent way).
General and Canonical Transformations
In the Hamiltonian approach, we're in phase space with a coordinate system having positions and momenta on an equal footing. It is therefore possible to think of more general transformations than the point transformation (which was restricted to the position coordinates).
We can have transformations that mix up position and momentum variables:
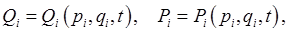
where ![]() ...
Read more »
...
Read more »
|
Maupertuis' Principle: Minimum Action Path at Fixed Energy
Divine Guidance
Incredibly, Maupertuis came up with a kind of principle of least action in 1747, long before the work of Lagrange and Hamilton. Maupertuis thought a body moved along a path such that the sum of products of mass, speed and displacement taken over time was minimized, and he saw that as the hand of God at work. This didn't go over well with his skeptical fellow countrymen, such as Voltaire, and in fact his formulation wasn't quite right, but history has given him partial credit, his name on a least action principle.
Suppose we are considering the motion of a particle moving around in a plane from some initial point and time 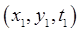 to some final to some final 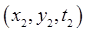 . Suppose its potential energy is a function of position, . Suppose its potential energy is a function of position, 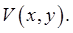 For example, imagine aiming for the hole on a rather bumpy putting green, but also requiring that the ball take a definite time, say two seconds, from being hit to falling in the hole. The action principle we've talked about so far will give the path, parameterized by time, For example, imagine aiming for the hole on a rather bumpy putting green, but also requiring that the ball take a definite time, say two seconds, from being hit to falling in the hole. The action principle we've talked about so far will give the path, parameterized by time,  ...
Read more »
...
Read more »
|
A New Way to Write the Action Integral
Introduction
Following Landau, we'll first find how the action integral responds to incremental changes in the endpoint coordinates and times, then use the result to write the action integral itself in a new, more intuitive way. This new formulation shows very directly the link to quantum mechanics, and variation of the action in this form gives Hamilton's equations immediately.
Function of Endpoint Position
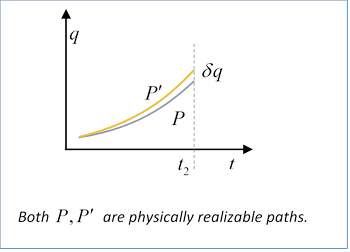 We'll now think of varying the action in a slightly different way. (Note: We're using Landau's notation.) Previously, we considered the integral of the Lagrangian over all possible different paths from the initial place and time We'll now think of varying the action in a slightly different way. (Note: We're using Landau's notation.) Previously, we considered the integral of the Lagrangian over all possible different paths from the initial place and time 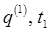 to the final place and time to the final place and time 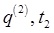 and found the path of minimum action. Now, though, we'll start with that path, the actual physical path, and investigate the corresponding action as a function of the final endpoint variables, given a fixed beginning place and time. and found the path of minimum action. Now, though, we'll start with that path, the actual physical path, and investigate the corresponding action as a function of the final endpoint variables, given a fixed beginning place and time.
Taking one degree of freedom (the generalization is straightfor
...
Read more »
|
Time Evolution in Phase Space: Poisson Brackets and Constants of the Motion
The Poisson Bracket
A function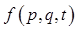 of the phase space coordinates of the system and time has total time derivative of the phase space coordinates of the system and time has total time derivative
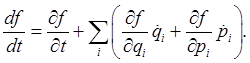
This is often written as
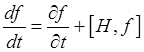
where
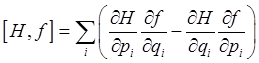
is called the Poisson bracket. (Warning! This is Landau's definition: many others use the opposite sign.)
If, for a phase space function 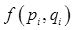 (that is, no explicit time dependence) (that is, no explicit time dependence) 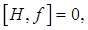 then then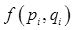 is a constant of the motion, also called an integral of the motion. is a constant of the motion, also called an integral of the motion.
In fact, the Poisson bracket can be defined for any two functio
...
Read more »
|
Mechanical Similarity and the Virial Theorem
Some Examples
Similar triangles are just scaled up (or down) versions of each other, meaning they have the same angles. Scaling means the same thing in a mechanical system: if a planet can go around the sun in a given elliptical orbit, another planet can go in a scaled up version of that ellipse (the sun remaining at the focus). But it will take longer: so we can't just scale the spatial dimensions, to get the same equation of motion we must scale time as well, and not in general by the same factor.
In fact, we can establish the relative scaling of space and time in this instance with very simple dimensional analysis. We know the planet's radial acceleration goes as the inverse square of the distance, so (radial acceleration)x(distance)2 = constant, the dimensionality of this expression is  , so , so  , the square of the time of one orbit is proportional to the cube of the size of the orbit. A little more explicitly, the acceleration , the square of the time of one orbit is proportional to the cube of the size of the orbit. A little more explicitly, the acceleration  so for the same so for the same  ...
Read more »
...
Read more »
|
Hamilton's Principle and Noether's Theorem
Introduction: Galileo and Newton
In the discussion of calculus of variations, we anticipated some basic dynamics, using the potential energy  for an element of the catenary, and conservation of energy for an element of the catenary, and conservation of energy  for motion along the brachistochrone. Of course, we haven't actually covered those things yet, but you're already very familiar with them from your undergraduate courses, and my aim was to give easily understood physical realizations of minimization problems, and to show how to find the minimal shapes using the calculus of variations. for motion along the brachistochrone. Of course, we haven't actually covered those things yet, but you're already very familiar with them from your undergraduate courses, and my aim was to give easily understood physical realizations of minimization problems, and to show how to find the minimal shapes using the calculus of variations.
At this point, we'll begin a full study of dynamics, starting with the laws of motion. The text, Landau, begins (page 2!) by stating that the laws come from the principle of least action, Hamilton's principle. This is certainly one possible approach, but confronted with it for the first time, one might well wonder where it came from. I prefer a gentler introduction, more or less following the historical order: Galileo, then Newton, then Lagrange and his colleagues, then Hamilton. The two approaches are of course equivalent. Naturally, you've seen most of this earlier stuff before, so here is a very brief s
...
Read more »
|
Fermat's Principle of Least Time
9/1/15
Another Minimization Problem
Here's another minimization problem from the 1600's, even earlier than the brachistochrone. Fermat famously stated in the 1630's that a ray of light going from point A to point B always takes the route of least time -- OK, it's trivially true in a single medium, light rays go in a straight line, but it's a lot less obvious if, say, A is in air and B in glass. Notice that this is closely related to our previous topic, the calculus of variations -- if this is a minimal time path, varying the path by a small amount will not change the time taken to first order. (Historical note: actually what amounted to Fermat's principle was first stated by Alhazen, in Baghdad, around 1000 AD.)
This seemed very mysterious when first extensively discussed, in the 1600's. In the last part of that century, and through the 1700's, Newton was the dominant figure, and he believed that light was a stream of particles. But how could the particle figure out the shortest time path from A to B?
In fact, there was one prominent physicist, Huygens, who thought light might be a wave. The main objection to this idea was that waves go around corners, at least to some extent, it seemed that light didn't. (Also, they exhibit diffraction effects, which no one thought they'd seen for light, although in fact Newton himself had observed diffrac
...
Read more »
|
The Calculus of Variations
Introduction
We've seen how Whewell solved the problem of the equilibrium shape of chain hanging between two places, by finding how the forces on a length of chain, the tension at the two ends and its weight, balanced. We're now going to look at a completely different approach: the equilibrium configuration is an energy minimum, so small deviations from it can only make second-order changes in the gravitational potential energy. Here we'll find how analyzing that leads to a differential equation for the curve, and how the technique developed can be successfully applied of a vast array of problems.
The Catenary and the Soap Film
The catenary is the curved configuration  of a uniform inextensible rope with two fixed endpoints at rest in a constant gravitational field. That is to say, it is the curve that minimizes the gravitational potential energy of a uniform inextensible rope with two fixed endpoints at rest in a constant gravitational field. That is to say, it is the curve that minimizes the gravitational potential energy
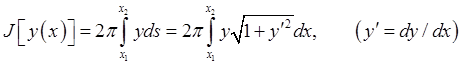
where we have taken the rope density and  both equal to unity for mathematical convenience. Usual
...
Read more » both equal to unity for mathematical convenience. Usual
...
Read more »
|
1. Introductory Lecture on Statics: the Catenary and the Arch
What? Statics?
Why begin a course on classical dynamics with a statics example? The reason is that the most important underlying principle of classical dynamics, and much of the rest of physics, is Hamilton’s Principle of Least Action: a system’s time development can always be describes as a path through some multidimensional parameter space (positions, velocities of all its component parts) and the path it actually follows is the one that (on varying the path) minimizes the integral of a certain function, called the action, along that path. A generalization of this principle by Dirac and Feynman (the "sum over paths") led to a fruitful reformulation of quantum mechanics and quantum field theory, now widely used.
The mathematical machinery necessary to minimize an integral along a path by varying the path is called the calculus of variations, so that’s what we have to master. To see how it works, we’ll first apply it to a simple example: finding the curve describing a uniform rope hanging between two points under gravity. The “action” for this statics problem is of course just the potential energy. And, to be sure we’ve found the right answer, we’ll first solve the problem by more traditional statics techniques. So this is where we begin.
The Catenary
What is the
...
Read more »
|
|