1:44 AM Motion of a Rigid Body: the Inertia Tensor | |
Motion of a Rigid Body: the Inertia TensorMichael Fowler Definition of RigidWe're thinking here of an idealized solid, in which the distance between any two internal points stays the same as the body moves around. That is, we ignore vibrations, or strains in the material resulting from inside or outside stresses. In fact, this is almost always an excellent approximation for ordinary solids subject to typical stresses -- obvious exceptions being rubber, flesh, etc. Following Landau, we'll usually begin by representing the body as a collection of particles of different masses Rotation of a Body about a Fixed Axis
(here
Evidently,
But notice that, assuming the rod is momentarily in the
The total angular momentum is not parallel to the total angular velocity! In fact, as should be evident, the total angular momentum is rotating around the constant angular velocity vector, so the axis must be providing a torque. This is why unbalanced car wheels stress the axle. General Motion of a Rotating Rigid BodyWe'll follow the Landau notation (which itself tends to be bilingual between coordinates We take a fixed, inertial (or lab) coordinate system labeled Suppose now that in infinitesimal time Therefore, the velocity in the fixed frame, writing the center of mass velocity
If the position of This means that if we describe the motion of any particle in the body in terms of some origin fixed in the body, plus rotation about that origin, the angular velocity vector describing the body's motion is the same irrespective of the origin we choose. So we can, without ambiguity, talk about the angular velocity of the body. From now on, we'll assume that the origin fixed in the body is at the center of mass. The Inertia TensorRegarding a rigid body as a system of individual particles, we find the kinetic energy
Now the first term,
Recall that (Alternatively, use the vector product identity The bottom line is that the kinetic energy
a translational kinetic energy plus a rotational kinetic energy. Warning about notation: at this point, things get a bit messy. The reason is that to make further progress in dealing with the rotational kinetic energy, we need to write it in terms of the individual components of the
The Landau's solution to the "too many suffixes for clarity" problem is to omit the suffix Double Suffix Summation Notation: to cut down on the number of
can be written as
But do not use Greek letters for dummy suffixes in this context: the standard is that they are used in relativistic equations to signify sums over the four dimensions of space time, Latin letters for sums over the three spatial dimensions, as we are doing here. The rotational kinetic energy is then
Warning: That first line is a bit confusing: copying Landau, I've written Anyway, moving on, we introduce the inertia tensor
in terms of which the kinetic energy of the moving, rotating rigid body is
As usual, the Lagrangian Landau writes the inertia tensor explicitly as
but you should bear in mind that Tensors 101We see that the "inertia tensor" defined above as
is a
Obviously, if we had chosen a different set of Cartesian axes from the same origin
This can be written more succinctly as
the bold font indicating a vector or matrix. In fact, a transformation from any set of Cartesian axes to any other set having the same origin is a rotation about some axis. This can easily be seen by first rotating so that the
so if the column vector
It might be worth spelling out explicitly here that the transpose of a square matrix (and almost all our matrices are square) is found by just swapping the rows and columns, or equivalently swapping elements which are the reflections of each other in the main diagonal, but the transpose of a vector, written as a column, has the same elements as a row, and the product of vectors follows the standard rules for matrix multiplication: Thus,
and
but
This will perhaps remind you of the Hilbert space vectors in quantum mechanics: the transposed vector above is analogous to the bra, the initial column vector being the ket. One difference from quantum mechanics is that all our vectors here are real, if that were not the case it would be natural to add complex conjugation to the transposition, to give The difference shown above between Definition of a TensorWe have a definite rule for how vector components transform under a change of basis: We'll do it in two parts, and one particle at a time. First, take that second term for one particle, it has the form
The same rotation matrix In fact, the inertia tensor is made up of elements exactly of this form in all nine places, plus diagonal terms
where Exercise: convince yourself that this is the same as This transformation property is the definition of a two-suffix Cartesian three-dimensional tensor: just as a vector in this space can be defined as an array of three components that are transformed under a change of basis by applying the rotation matrix,
Writing this in matrix notation, and keeping an eye on the indices, we see that with the standard definition of a matrix product,
(The transformation property for our tensor followed immediately from that for a vector, since our tensor is constructed from vectors, but by definition the same rule applies to all Cartesian tensors, which are not always expressible in terms of vector components.) Diagonalizing the Inertia TensorThe inertia tensor has the form of a real symmetric matrix. By an appropriate choice of axes
These axes, with respect to which the inertia tensor is diagonal, are called the principal axes of inertia, the moments about them If you're already familiar with the routine for diagonalizing a real symmetric matrix, you can skip this review. The diagonalization of the tensor/matrix proceeds as follows. First, find the eigenvalues
(The Now since
The left hand side is a real number: this can be established by taking its complex conjugate. The fact that the tensor is real and symmetric is crucial!
And since these are dummy suffixes, we can swap the (Note: a real symmetric matrix does not necessarily have positive roots: for example Taking the eigenvalues to be distinct (the degenerate case is easy to deal with) the eigenvectors are orthogonal, by the standard proof, for this matrix left eigenvectors (rows) have the same eigenvalues as their transpose, so
and The diagonalizing matrix is made up of these eigenvectors (assumed normalized):
a column of row vectors. To check that this is indeed a rotation vector, from one orthogonal set of axes to another, notice first that its transpose Now apply this
In vector language, these elements are just We can confirm this by applying the rotation to the inertia tensor itself:
Let's examine the contribution of one particle to the inertia tensor:
Note that The transformation is
.
We've dropped the primes, since we'll be working in this natural frame from now on. Principal Axes Form of Moment of Inertia TensorWe already know that the transformed matrix is diagonal, so its form has to be
The moments of inertia, the diagonal elements, are of course all positive. Note that no one of them can exceed the sum of the other two, although it can be equal in the (idealized) case of a two-dimensional object. For the two-dimensional case, taking the body to lie in the
. Relating Angular Momentum to Angular VelocityIt's easy to check that the angular momentum vector
just by writing it out explicitly:
Exercise: check this by putting in all the suffixes. Symmetries, Other Axes, the Parallel Axis TheoremIf a body has an axis of symmetry, the center of mass must be on that axis, and it is a principal axis of inertia. To prove the center of mass statement, note that the body is made up of pairs of equal mass particles on opposite sides of the axis, each pair having its center of mass on the axis, and the body's center of mass is that of all these pairs centers of mass, all of which are on the axis. Taking this axis to be the The moment of inertia about an arbitrary axis through the center of mass, in the direction of the unit vector
The inertia tensor about some origin
In particular, we have the parallel axis theorem: the moment of inertia about any axis through some point | |
|
| |
| Total comments: 0 | |
 As a preliminary, let's look at a body firmly attached to a rod fixed in space, and rotating with angular velocity
As a preliminary, let's look at a body firmly attached to a rod fixed in space, and rotating with angular velocity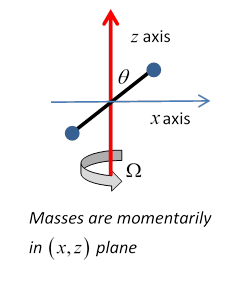 But you also know that both angular velocity and angular momentum are vectors. Obviously, for this example, the angular velocity is a vector pointing along the axis of rotation,
But you also know that both angular velocity and angular momentum are vectors. Obviously, for this example, the angular velocity is a vector pointing along the axis of rotation,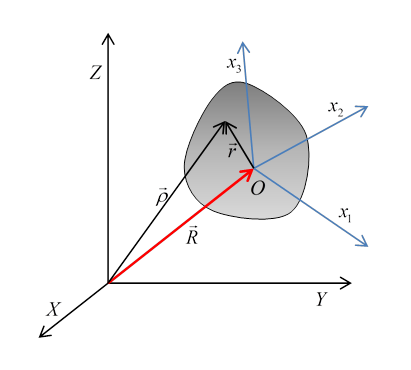 Now, in deriving the above equation, we have not used the fact that the origin
Now, in deriving the above equation, we have not used the fact that the origin 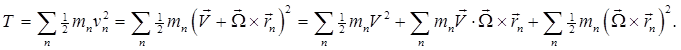
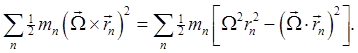
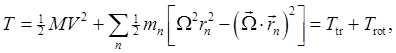
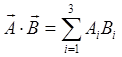
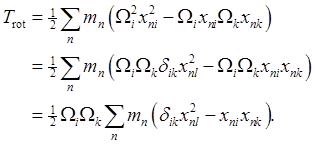
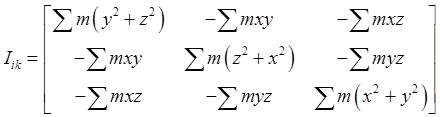

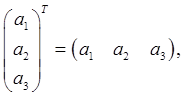


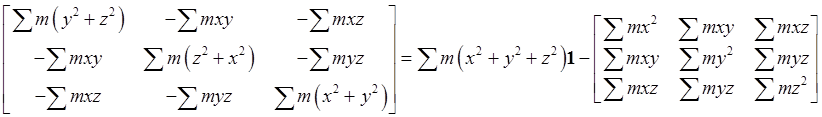
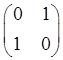 .)
.)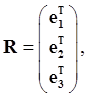
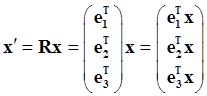 .
.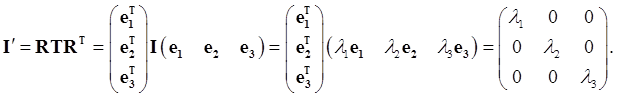
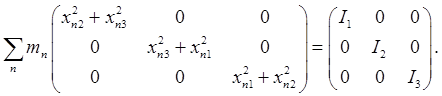
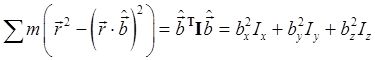 .
.