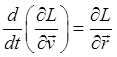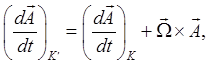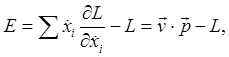Motion in a Non-inertial Frame of Reference

Michael Fowler

The Lagrangian in Accelerating and Rotating Frames

This section concerns the motion of a single particle in some potential  in a non-inertial frame of reference. (We'll use rather than  for potential in this section, since we'll be using  for relative frame velocity.) The most general noninertial frame has both linear acceleration and rotation, and the angular velocity of rotation may itself be changing.

Our strategy is to begin with an inertial frame  then go to a frame  having linear acceleration relative to  then finally to a frame  rotating relative to  We will construct the Lagrangian in  and from it the equations of motion in that noninertial frame.

First, suppose the noninertial frame  to be moving relative to  at time-varying velocity 

In the inertial frame the Lagrangian is as usual

so Lagrange's equations give the standard result,

the subscript  denoting quantities in this inertial frame.

The Principle of Least Action is a frame-independent concept, so the calculus of variations Lagrangian equations it leads to,

must also be correct in a non-inertial frame.

How can this be true? The reason is that in a non-inertial frame, the Lagrangian has a different form.

To find the Lagrangian in terms of the velocity meaning the velocity measured in the frame , we just insert

into  giving the Lagrangian  in the accelerating frame :

Following Landau,  is purely a function of time, so can be expressed as the derivative of a function of time, recall terms of that form do not affect the minimization of the action giving the equations of motion, and so can be dropped from the Lagrangian.

The second term,

Again, the total derivative term can be dropped, giving

from which the equation of motion is

Landau writes this as

So the motion in the accelerating frame is the same as if an extra force is added -- this extra force is just the product of the particle's mass and the frame's acceleration, it's just the "force" that pushes you back in your seat when you step on the gas, the linear equivalent of the "centrifugal force" in a rotating frame.

Speaking of centrifugal force, we now bring in our final frame , having the same origin as , (so we can take at a given instant) but rotating relative to it with angular velocity 

What is the Lagrangian translated intovariables? The velocities in  are related by

and, putting this in the Lagrangian above,

From this,

.

(Note that this is the canonical momentum, .)

Using

,

we have

The equation of motion

is therefore:

The equation of motion of a particle in a rotating frame can also be found directly, without using the Lagrangian approach.  Suppose  is a fixed frame, and  is rotating relative to  with angular velocity   Then some time-dependent vector  in  will have a rate of change in  given by

and its acceleration is

For a particle in the Earth's gravitational field (discussed below), the true acceleration (fixed frame)  is the left-hand side, measured in coordinates in the Earth's rotating frame  (the right-hand side), we have

and the last two terms are negligible in this context.   

Uniformly Rotating Frame

For the important case of a frame having uniform rotation and no translation motion,

The last term is (as Landau states) the "centrifugal force", but this term is now politically incorrect, since it isn't a "real force", just an effect of being in a rotating frame. (It's still OK to say gravitational force, though, although that isn't a real force either, I guess, since it disappears in the local inertial "freely falling" frame, as was first noticed by Galileo, and centuries later by Einstein, who called it "the happiest thought of my life".)

The second term, , Landau calls the Coriolis force. (Again, the politically correct tend to talk about the Coriolis effect, meaning deviation of a projectile, say, from an inertial frame trajectory resulting from the operation of this "force".) A very nice illustration of this "force" is in the Frames of Reference 2 movie, starting at time 3:50.

Notice the Coriolis force depends on the velocity of the particle, and is reminiscent of the magnetic force on a charged particle. For example, it does no work on the particle, but does curve the particle's path.

The energy of the particle can be found from the standard Lagrangian equation

where

This is interesting! Remembering  the momentum, defined in this way as a canonical variable, not as just in the frame we're in, is the same in the two frames 

The angular momenta  and  are also equal in the two frames.

The Lagrangian is

so

The new term is the centrifugal potential energy. It's negative because it takes work to bring something towards the axis of rotation. To see how this energy relates to the energy in the original fixed frame, substitute in this equation  to find

true for one particle, and by addition for any system of particles.

Exercise: check this: note that  Notice the difference can be positive or negative -- give a simple one-particle illustration of this.

Coriolis Effect: Particle Moving near Earth's Surface

The Earth's surface is a rotating frame of reference, but the angular velocity is sufficiently small that we can often drop second order terms. Recall the equation of motion in a rotating frame is

which becomes, close to the Earth and dropping the second-order term,

The leading order solution, ignoring the small rotation term, is the familiar

.

The second term is much smaller than the first, so it's OK to replace the there by , and to find the leading correction to the path put

in the equation  giving

The full equation can now be integrated to give

Let's try some numbers: in 1803, an experiment was conducted in Schlebusch, Germany that attracted the interest of the scientific community. Twenty-nine iron pebbles were dropped into a 90-meter deep mineshaft.

In 1831 the experiment was repeated in a 158.5 m deep mine in Freiburg, Saxony. From 106 drops an average deflection of 28.3 mm was estimated, close to the theoretical value of 27.5 mm. (This agrees exactly with our formula, from Landau's book.)

Exercise: where would you expect the particle to fall, compared with a straight down plumb line? To make visualizing a little easier, imagine the mine to be on the equator. Then the ground is moving east faster than the bottom of the mine -- so the pebble will fall to the east.

Naval gunnery: HMS Dreadnought, 1906: the BL 12 inch Mk X gun. Shells at 800 m/sec, range about 23 km. For vertical velocity of say 400 m/sec, time in air of order 80 secs. The two terms are about equal magnitude, around 100 meters.

I pick this ship because there is a rumor that in a 1915 naval battle near the Falkland islands, off Argentina, between the British and German navies, the British kept missing because they corrected their aim for Coriolis deflections appropriate to the northern hemisphere. I'm not sure if it's true.

Gyroscopes and Gyrocompasses in Navigation

A gyroscope is a fast-spinning disc supported in such a way that there is no external torque, except an occasional boost to keep up its speed (jet of air, or magnetic). Since there is no external torque, it always points the same way. A device based on this principle and used in aircraft is termed a heading indicator.

Suppose the gyroscope is set spinning about an initially vertical axis. If it's nighttime, this means its axis is pointing to a particular star, overhead at that moment. It will continue to point to that star, so, unless you're at the North or South Pole, the axis will move from the local vertical to return 24 hours later. Since the direction of the gyroscope axis is fixed in space, and the Earth's axis of rotation is fixed in space, the angle between the two is obviously constant, so as seen in the lab, say, the gyroscope axis describes a cone about a line parallel to the axis (the line a sundial pointer points along, vertical at the North Pole (so the gyro doesn't change) down to horizontal at the Equator.

This is useful, but it would be better to have a pointer that just points North (or South). This is achieved by damping the gyroscopes motion -- put one end in viscous liquid. Then, when it moves relative to its container, there is a couple opposing the motion. What this does is move it inwards, relative to its cone of motion, that is, the cone shrinks, so it goes to a stable orientation parallel to the Earth's axis, that is, it points North (or South).

A gyrocompass is the same idea, but now constrained to lie in a horizontal plane. This plus some damping forces the compass to orient as close to the Earth's axis as possible in the horizontal plane, meaning it points North, in this hemisphere.