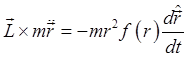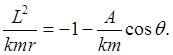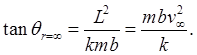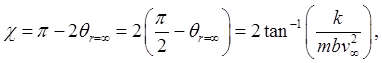1:33 AM Elastic Scattering | |
Elastic ScatteringMichael Fowler Billiard Balls"Elastic" means no internal energy modes of the scatterer or of the scatteree are excited -- so total kinetic energy is conserved. As a simple first exercise, think of two billiard balls colliding. The best way to see it is in the center of mass frame of reference. If they're equal mass, they come in from opposite directions, scatter, then move off in opposite directions. In the early days of particle accelerators (before colliders) a beam of particles was directed at a stationary target. So, the frame in which one particle is initially at rest is called the lab frame. What happens if we shoot one billiard ball at another which is initially at rest? (We'll ignore possible internal energies, including spinning.) The answer is that they come off at right angles. This follows trivially from conservation of energy and momentum (in an obvious notation)
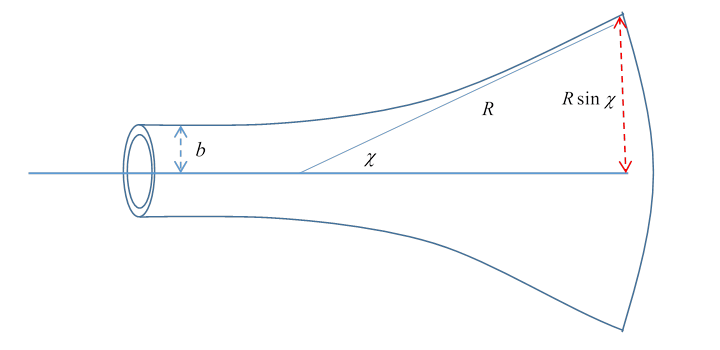
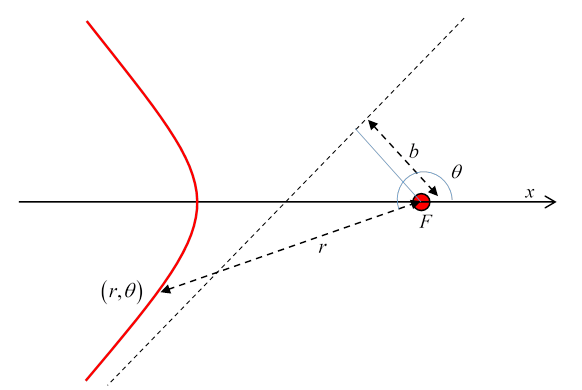
and Pythagoras' theorem. Discovery of the NucleusThe first significant use of scattering to learn about the internal structure of matter was Rutherford's use of For To visualize what's going on, think of the scatterer as a bowling ball with tiny marbles directed towards it, they're moving fast horizontally, along parallel but random paths. (Let's take zero gravity here -- the We observe the rate at which marbles are being scattered in various directions. Call the scattering angle So, let's assume the width of the "beam" of marbles is much greater than the size of the bowling ball. We'll also take the intensity of the beam to be uniform, with Now, if the bowling ball has radius The Differential Cross SectionIn a real scattering experiment, information about the scatterer can be figured out from the different rates of scattering to different angles. Detectors are placed at various angles The differential cross section, written Now, we'll assume the potential is spherically symmetric. Imagine a line parallel to the incoming particles going through the center of the atom. For a given ingoing particle, its impact parameter is defined as the distance its ingoing line of flight is from this central line. Landau calls this A particle coming in with impact parameter between Note: we've switched for this occasion from
So, an ingoing cross section Therefore the scattering differential cross section
(Note that Analyzing Inverse-Square Repulsive Scattering: Kepler AgainTo make further progress, we must calculate Recall our equation for Kepler orbits:
Let's now switch from gravitational scattering with an attractive force
say. Since this is repulsive, the sign will change in the radial acceleration equation,
Also, we want the scattering parameterized in terms of the impact parameter
So just as with the Kepler problem, the orbit is given by
say. From the lecture on Orbital Mathematics, the polar equation for the left hyperbola branch relative to the external (right) focus is
this is a branch symmetric about the
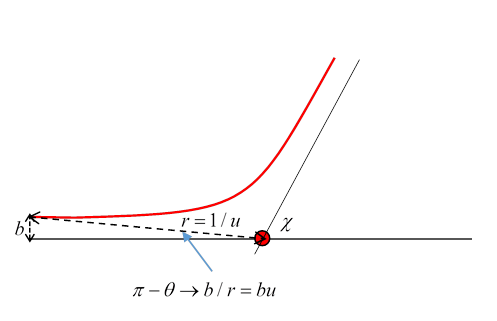
But we want the incoming branch to be parallel to the axis, which we do by suitable choice of In other words, we rotate the hyperbola clockwise through half the angle between its asymptotes, keeping the scattering center (right-hand focus) fixed. From the lecture on orbital mathematics (last page), the perpendicular distance from the focus to the asymptote is the hyperbola parameter Hence the particle goes in a hyperbolic path with parameters We can, however, fix the path uniquely by equating the leading order correction to the incoming zeroth order straight path: the particle is coming in parallel to the
In this small
Matching the zeroth order and the first order terms
eliminates
So this is the scattering angle in terms of the impact parameter
Equivalently,
so
and the incremental cross sectional area
This is Rutherford's formula: the incremental cross section for scattering into an incremental solid angle, the differential cross section
(Recall
Vectorial Derivation of the Scattering Angle(from Milne) The essential result of the above analysis was the scattering angle as a function of impact parameter, for a given incoming energy. It's worth noting that this can be found more directly by vectorial methods from Hamilton's equation. Recall from the last lecture Hamilton's equation
and the integral for an inverse square force
As previously discussed, multiplying by
This corresponds to the equation
(the left-hand branch with the right-hand focus as origin, note from diagram above that
To find the scattering angle, suppose the unit vector pointing parallel to the asymptote is Note that as before,
We're not rotating the hyperbola as we did in the alternative treatment above: here we keep it symmetric about the Now take Hamilton's equation in the asymptotic limit, where the velocity is parallel to the displacement: the vector product of Hamilton's equation
It follows that
And together with
This is the angle between the asymptote and the major axis: the scattering angle
agreeing with the previous result. | |
|
| |
| Total comments: 0 | |
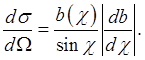
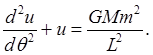

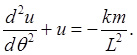

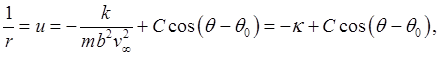
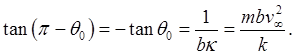


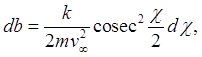
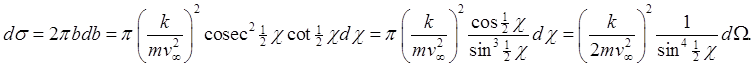 .
.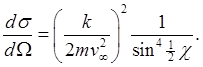
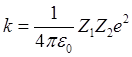 in MKS units.)
in MKS units.)