1:41 AM Parametric Resonance | |
Parametric ResonanceMichael Fowler Introduction(Following Landau para 27) A one-dimensional simple harmonic oscillator, a mass on a spring,
has two parameters, We are interested here in the system's response to some externally imposed periodic variation of its parameters, and in particular we'll be looking at resonant response, meaning large response to a small imposed variation. Note first that imposed variation in the mass term is easily dealt with, by simply redefining the time variable to Then
and the equation of motion becomes
This means we can always transform the equation so all the parametric variation is in the spring constant, so we'll just analyze the equation
Furthermore, since we're looking for resonance phenomena, we will only consider a small parametric variation at a single frequency, that is, we'll take
where (Note: We prefer We have now a driven oscillator:
How does this differ from our previous analysis of a driven oscillator? In a very important way! The amplitude For one thing, this means that if the oscillator is initially at rest, it stays that way, in contrast to an ordinary externally driven oscillator. But if the amplitude increases, so does the driving force. This can lead to an exponential increase in amplitude, unlike the linear increase we found earlier with an external driver. (Of course, in a real system, friction and nonlinear potential terms will limit the growth.) What frequencies will prove important in driving the oscillator to large amplitude? It responds best, of course, to its natural frequency
with no component at the natural frequency The simplest way to get resonance is to take Resonance near Double the Natural FrequencyFrom the above argument, the place to look for resonance is close to
and, bearing in mind that we're looking for oscillations close to the natural frequency, puts in
with It's important to realize that this is an approximate approach. It neglects nonresonant frequencies which must be present in small amounts, for example
and the And, since the assumption is that
This must equal
Keeping only the resonant terms, we take
The equation becomes:
The zeroth-order terms cancel between the two sides, leaving
Collecting the terms in
The sine and cosine can't cancel each other, so the two coefficients must both be identically zero. This gives two first order differential equations for the functions
The amplitude growth rate is therefore
Parametric resonance will take place if
a band of width Example: Pendulum Driven at near Double the Natural FrequencyA simple pendulum of length
The Lagrangian
The purely time-dependent term will not affect the equations of motion, so we drop it, and since the equations are not affected by adding a total derivative to the Lagrangian, we can integrate the second term by parts (meaning we're dropping a term
(We've also dropped the term The equation for small oscillations is
Comparing this with
we see that | |
|
| |
| Total comments: 0 | |
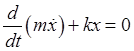

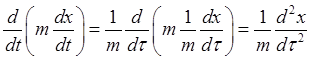 ,
,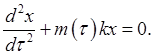



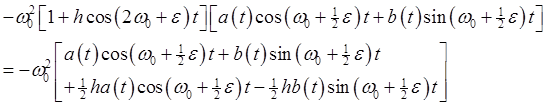
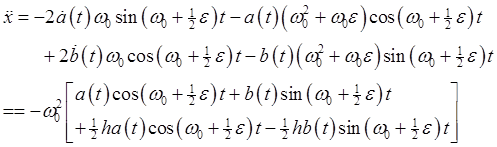

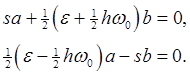
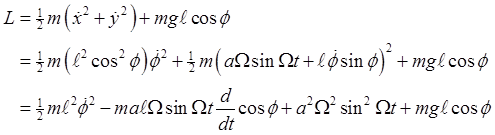
 ) to get
) to get