1:35 AM Driven Oscillator | |
Driven OscillatorMichael Fowler (closely following Landau para 22) Consider a one-dimensional simple harmonic oscillator with a variable external force acting, so the equation of motion is
which would come from the Lagrangian
(Landau "derives" this as the leading order non-constant term in a time-dependent external potential.) The general solution of the differential equation is An important case is that of a periodic driving force
But what happens when
The second term now goes to
The amplitude of the oscillations grows linearly with time. Obviously, this small oscillations theory will crash eventually. But what if the external force frequency is slightly off resonance? Then (real part understood)
with The wave amplitude squared
We're seeing beats, with beat frequency Energy is exchanged back and forth with the driving external force. More General Energy ExchangeWe'll derive a formula for the energy fed into an oscillator by an arbitrary time-dependent external force. The equation of motion can be written
and defining
This first-order equation integrates to
The energy of the oscillator is
So if we drive the oscillator over all time, with beginning energy zero,
This is equivalent to the quantum mechanical time-dependent perturbation theory result: Damped Driven OscillatorThe linear damped driven oscillator:
(Following Landau's notation here -- note it means the actual frictional drag force is Looking near resonance for steady state solutions at the driving frequency, with amplitude
For a near-resonant driving frequency
so the response, the dependence of amplitude of oscillation on frequency, is to this accuracy
(We might also note that the resonant frequency is itself lowered by the damping, but this is another second-order effect we ignore here.)
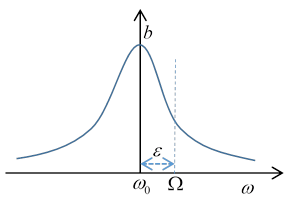
The half width of the resonance curve as a function of driving frequency For future use, we'll write the above equation for the amplitude as
| |
|
| |
| Total comments: 0 | |
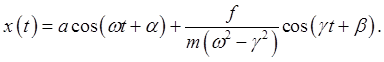

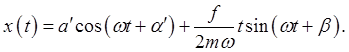
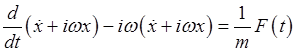
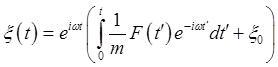
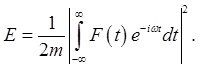
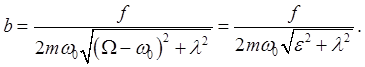
 The rate of absorption of energy equals the frictional loss. The friction force
The rate of absorption of energy equals the frictional loss. The friction force  .
.