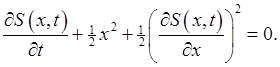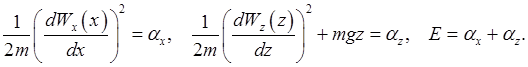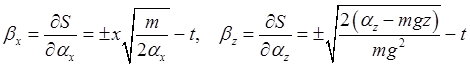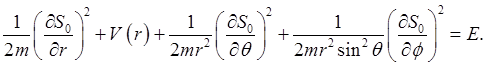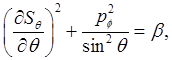The Hamilton-Jacobi Equation

Michael Fowler

Back to Configuration Space

We've established that the action, regarded as a function of its coordinate endpoints and time, satisfies

and at the same time so obeys the first-order differential equation

This is the Hamilton-Jacobi equation.

Notice that we're now back in configuration space!

For example, the Hamilton-Jacobi equation for the simple harmonic oscillator in one dimension is

(Notice that this has some resemblance to the Schrödinger equation for the same system.)

If the Hamiltonian has no explicit time dependence  becomes just  so the action has the form , and the Hamilton-Jacobi equation is

(This is analogous to the time independent Schrödinger equation for energy eigenstates.)

The Hamilton-Jacobi equation is therefore a third complete description of the dynamics, equivalent to Lagrange's equations and to Hamilton's equations.

Since  only appears differentiated, if we have a solution to the equation, we can always add an arbitrary constant term, to give an equally valid solution. For the general case, there will be a furtherconstants of integration, so a complete solution has the form

the  andbeing the constants of integration. We're not saying it's easy to solve this differential in general, just that we know how many constants of integration there must be in a final solution. Since the action determines the motion of the system completely, the constants of integration will be determined by the given initial and final coordinates, or, they could equally be regarded as functions of the initial coordinates and momenta (the initial momenta themselves being determined by the given initial and final coordinates).

The Central Role of These Constants of Integration

To describe the time development of a dynamical system in the simplest way possible, it is desirable to find parameters that are constant or change in a simple way. For example, motion in a spherically symmetric potential is described in terms of (constant) angular momentum components.

Now, these constantare functions of the initial coordinates and momenta. Since they remain constant during the motion, they are evidently among the "variables" that describe the dynamical development in the simplest possible way. So, we need to construct a canonical transformation from our current set of variables (final coordinates and momenta) to a new set of variables that includes these constant of integration "momenta". (The corresponding canonical "positions" will then be given by differentiating the generating function with respect to the "momenta".)

How do we find the generating function for this transformation? A clue comes from one we've already discussed: that corresponding to development in time, going from the initial set of variables to the final set, or back. That transformation was generated by the action itself, expressed in terms of the two sets of positions. That is, we allowed both ends of the action integral path to vary, and wrote the action as a function of the finaland initial endpoint variables and times:

In the present section, the final endpoint positions are denoted simply by these are the same as the earlier  . Explicitly, we're writing

Compare this expression for the action with the formal expression we just derived from the Hamilton Jacobi equation,

These two expressions forhave just the same form: the action is expressed as a function of the endpoint position variables, plus anothervariables needed to determine the motion uniquely. This time, instead of the original position variables, though, the second set of variables is these constants of integration, the's.

Now, just as we showed the action generated the transformation (either way) between the initial set of coordinates and momenta and the final set, it will also generate a canonical transformation from the final set of coordinates and momenta to another canonical set, having the  's as the new "momenta". We'll label the new "coordinates" (the canonical conjugates of the's)  .

Taking then the action (neglecting the constantwhich does nothing)  as the generating function, it depends on the old coordinatesand the new momenta. This is the same set of variables -- old coordinates and new momenta -- as those of the (previously discussed) generating function 

Recall

,

so here

,

and

This defines the new "coordinates", and ensures that the transformation is canonical.

To find the new Hamiltonian, we need to find  and add it to

But

where is just a constant, so

The first equation in this section was

so the new Hamiltonian

We have made a canonical transformation that has led to a zero Hamiltonian!

What does that mean? It means that the neither the new momenta nor the new coordinates vary in time:

.

(The fact that all momenta and coordinates are fixed in this representation does not mean that the system doesn't move -- as will become evident in the following simple example, the original coordinates are functions of these new (nonvarying!) variables and time.)

The  equations  can then be used to find the  as functions of . To see how all this works, it is necessary to work through an example.

A Simple Example of the Hamilton-Jacobi Equation: Motion Under Gravity

The Hamiltonian for motion under gravity in a vertical plane is

so the Hamilton-Jacobi equation is

First, this Hamiltonian has no explicit time dependence (gravity isn't changing!), so from we can replace the last term in the equation by 

A Simple Separation of Variables

Since the potential energy term depends only on the equation is solvable using separation of variables. To see this works, try

Putting this form into the equation, the resulting first term depends only on the variable the second plus third depend only on, the last term is just the constant A function depending only oncan only equal a function independent of  if both are constants, similarly for

Labeling the constants,

So these's are constants of the motion, they are our new "momenta" (although they have dimensions of energy).

Solving,

(We could add in constants of integration, but adding constants to the action changes nothing.)

So now we have

This is our generating function (equivalent to ), in terms of old coordinates and these new "momenta",  Following the Hamilton-Jacobi analysis, this action will generate a canonical transformation which reduces the Hamiltonian to zero, meaning that not only these new momenta stay constant, but so do their conjugate "coordinate" variables,

These equations solve the problem. Rearranging, the trajectory is

The four "constants of motion"are uniquely fixed by the initial coordinates and velocities, and they parameterize the subsequent time evolution of the system.

Separation of Variables for a Central Potential; Cyclic Variables

Landau presents in some details the separation of variables method for a  potential, interesting here because it results in equations you've met before -- those arising in the standard quantum treatment of the hydrogen atom.

How do we make any progress with these formidable differential equations? One possibility is that some coordinates are cyclic, meaning that say, does not appear explicitly in the Hamiltonian -- for example, an angle variable in a spherically symmetric field. Then we have immediately that the corresponding momentum,  a constant.

The Hamiltonian for a central potential is:

The Hamilton-Jacobi equation is therefore

The first thing to note is thatis cyclic (it doesn't appear in the Hamiltonian), so we can immediately replace  with a constant

Then we have:

Now we seek a solution of the form

Substituting in the equation, notice that the expression in square brackets will become

independent of but on multiplying the full equation by , and staring at the result, we see that in fact it is purely a function of  This means that it's a constant, say

and then

These first-order equations can then be solved, at least numerically (and of course exactly for some cases). Physically,  being the total angular momentum, and is the total energy.

Note: recall that in quantum mechanics, for example in solving the Schrödinger equation for the hydrogen atom, the separation of variables was achieved by writing the wave function as a product of functions belonging to the different variables. Here we use a sum -- remember that the action corresponds closely to the phase of a quantum mechanical system, so a sum of actions is analogous to a product of wave functions.