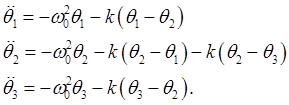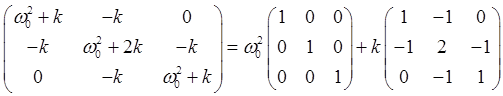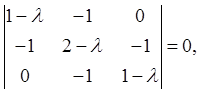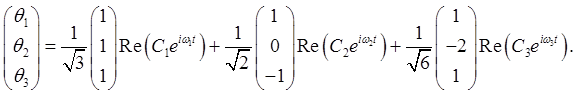1:34 AM Small Oscillations | |
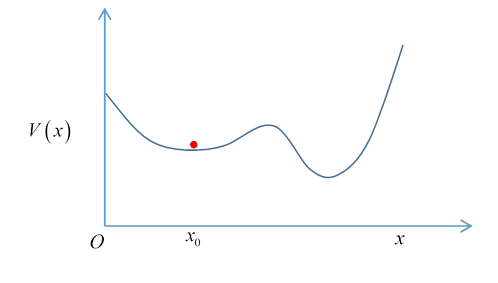
Small OscillationsMichael Fowler Particle in a WellWe begin with the one-dimensional case of a particle oscillating about a local minimum of the potential energy To simplify the equations, we'll also move the
replacing the second derivative with the standard "spring constant" expression. This equation has solution
(This can, of course, also be derived from the Lagrangian, easily shown to be Two Coupled PendulumsWe'll take two equal pendulums, coupled by a light spring. We take the spring restoring force to be directly proportional to the angular difference between the pendulums. (This turns out to be a good approximation.) For small angles of oscillation, we take the Lagrangian to be
Denoting the single pendulum frequency by
We look for a periodic solution, writing
(The final physical angle solutions will be the real part.) The equations become (in matrix notation):
Denoting the
This is an eigenvector equation, with
Solving,
The corresponding eigenvectors are Normal ModesThe physical motion corresponding to the amplitudes eigenvector
with Clearly, this is the mode in which the two pendulums are in sync, oscillating at their natural frequency, with the spring playing no role. In physics, this mathematical eigenstate of the matrix is called a normal mode of oscillation. In a normal mode, all parts of the system oscillate at a single frequency, given by the eigenvalue. The other normal mode,
where we have written The matrix structure can be clarified by separating out the spring contribution:
All vectors are eigenvectors of the identity, of course, so the first matrix just contributes Principle of SuperpositionThe equations of motion are linear equations, meaning that if you multiply a solution by a constant, that's still a solution, and if you have two different solutions to the equation, the sum of the two is also a solution. This is called the principle of superposition. The general motion of the system is therefore
where it is understood that This is a four-parameter solution: the initial positions and velocities can be set arbitrarily, completely determining the motion. Exercise: begin with one pendulum straight down, the other displaced, both momentarily at rest. Find values for Solution: At The solution for the motion of the first pendulum is
and for small
Here the pendulum is oscillating at approximately To think about: What happens if the two have different masses? Do we still get these beats -- can the larger pendulum transfer all its kinetic energy to the smaller? Exercise: try pendulums of different lengths, hung so the bobs are at the same level, small oscillation amplitude, same spring as above. Three Coupled PendulumsLet's now move on to the case of three equal mass coupled pendulums, the middle one connected to the other two, but they're not connected to each other. The Lagrangian is
Putting
The equations of motion are
Putting
The normal modes of oscillation are given by the eigenstates of that second matrix. The one obvious normal mode is all the pendulums swinging together, at the original frequency The full eigenvalue equation is
that is, The normal mode eigenvectors satisfy
They are The equations of motion are linear, so the general solution is a superposition of the normal modes:
Normal CoordinatesLandau writes
It's worth going through the exercise of writing the Lagrangian in terms of the normal coordinates: recall
Putting in the above expressions for the
We've achieved a separation of variables. The Lagrangian is manifestly a sum of three simple harmonic oscillators, which can have independent amplitudes and phases. Incidentally, this directly leads to the action angle variables -- recall that for a simple harmonic oscillator the action Three Equal Pendulums Equally CoupledWhat if we had a third identical spring connecting the two end pendulums (we could have small rods extending down so the spring went below the middle pendulum? What would the modes of oscillation look like in this case? Obviously, all three swinging together is still an option, the eigenvector
The equation for the eigenvalues is easily found to be Think about the physical situation. If we set the first two pendulums swinging exactly out of phase, the third pendulum will feel no net force, so will stay at rest. But we could equally choose another pair. And, the eigenvector | |
|
| |
| Total comments: 0 | |

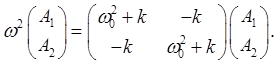

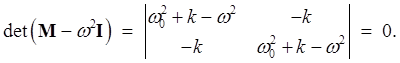
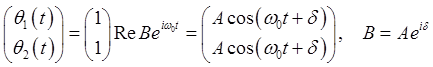
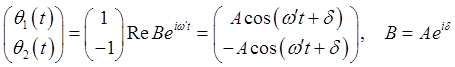
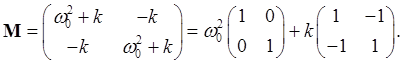

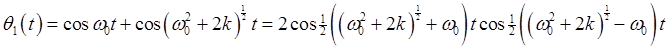 .
.