1:12 AM Introduction to Liouville's Theorem | |
Introduction to Liouville's TheoremPaths in Simple Phase Spaces: the SHO and Falling BodiesLet's first think further about paths in phase space. For example, the simple harmonic oscillator, with Hamiltonian Question: are these circles the only possible paths for the oscillator to follow? Answer: yes: any other path would intersect a circle, and at that point, with both position and velocity defined, there is only one path forward (and back) in time possible, so the intersection can't happen.
Check: convince yourself that all these paths are parts of parabolas centered on the Bodies released with the same initial velocity at the same time will keep the same vertical distance apart, those released with different initial velocities will keep the same velocity difference, since all accelerate at Exercise: convince yourself that all the points of an initial vertical side of the square all stay in line as time goes on, even though the line does not stay vertical. The four sides of the square deform with time to the four sides of the parallelogram, point by point. This means that if we have a falling stone corresponding initially to a point inside the square, it will go to a point inside the parallelogram, because if somehow its path reached the boundary, we would have two paths in phase space intersecting, and a particle at one point in phase space has a uniquely defined future path (and past). Following Many Systems: a "Gas" in Phase SpaceWe've looked at four paths in phase space, corresponding to four falling bodies, all beginning at The argument above about the phase space path of a point within the square at if at t = 0 some closed surface in phase space contains a number of points of the gas, those same points remain inside the surface as it develops in time -- none exit or enter. For the number of points Liouville's Theorem: Local Gas Density Is Constant along a Phase Space PathThe falling bodies phase space square has one more lesson for us: visualize now a uniformly dense gas of points inside the initial square. Not only does the gas stay within the distorting square, the area it covers in phase space remains constant, as discussed above, so the local gas density stays constant as the gas flows through phase space. Liouville's theorem is that this constancy of local density is true for general dynamical systems. Landau's Proof Using the JacobianLandau gives a very elegant proof of elemental volume invariance under a general canonical transformation, proving the Jacobian multiplicative factor is always unity, by clever use of the generating function of the canonical transformation. Jacobians have wide applicability in different areas of physics, so this is a good time to review their basic properties, which we do below, as a preliminary to giving the proof. It must be admitted that there are simpler ways of deriving Liouville's theorem, directly from Hamilton's equations, the reader may prefer to skip the Jacobian proof at first reading. Jacobian for Time EvolutionAs we've established, time development is equivalent to a canonical coordinate transformation,
Since we already know that the number of points inside a closed volume is constant in time, Liouville's theorem is proved if we can show that the volume enclosed by the closed surface is constant, that is, with
If you're familiar with Jacobians, you know that (by definition)
where the Jacobian
Liouville's theorem is therefore proved if we can establish that Jacobians 101You can skip this section if you're already familiar with Jacobians. Suppose we are integrating a function over some region of ordinary three-dimensional space,
but we want to change variables of integration to a different set of coordinates We need to think carefully about the volumes in the three-dimensional space represented by For the Hence, in components,
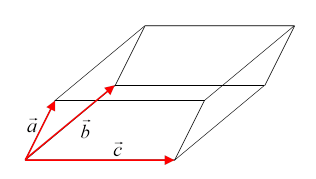
Now the volume of the parallelepiped with sides the three vectors from the origin So, the volume corresponding to the increments
writing The standard notation for this determinantal Jacobian is
So the appropriate replacement for the three dimensional incremental volume element represented in the integral by
The inverse
this is easily established using the chain rule for differentiation. Exercise: check this! Thus the change of variables in an integral is accomplished by rewriting the integrand in the new variables, and replacing
The argument in higher dimensions is just the same: on going to dimension We've seen that the chain rule for differentiation gives the inverse as just the Jacobian with numerator and denominator reversed, it also readily yields
and this extends trivially to It's also evident form the determinantal form of the Jacobian that
identical variables in numerator and denominator can be canceled. Again, this extends easily to Jacobian proof of Liouville's TheoremAfter this rather long detour into Jacobian theory, recall we are trying to establish that the volume of a region in phase space is unaffected by a canonical transformation, we need to prove that
and that means we need to show that the Jacobian
Using the theorems above about the inverse of a Jacobian and the chain rule product,
Now invoking the rule that if the same variables appear in both numerator and denominator, they can be cancelled,
Up to this point, the equations are valid for any nonsingular transformation -- but to prove the numerator and denominator are equal in this expression requires that the equation be canonical, that is, be given by a generating function, as explained earlier. Recall now the properties of the generating function
from which
In the expression for the Jacobian In terms of the generating function Exactly the same procedure for the denominator gives the
In other words, the two determinants are the same (rows and columns are switched, but that doesn't affect the value of a determinant). This means Simpler Proof of Liouville's TheoremLandau's proof given above is extremely elegant: since phase space paths cannot intersect, point inside a volume stay inside, no matter how the volume contorts, and since time development is a canonical transformation, the total volume, given by integrating over volume elements
The points here represent a "gas" of many systems in the two dimensional Begin with the top edge: the particles are all moving with velocities Adding in the other two edges (the sides), with an exactly similar argument, the total area change is
But from Hamilton's equations
and therefore
establishing that the total incremental area change as the square distorts is zero. The conclusion is that the flow of the gas of systems in phase space is like an incompressible fluid, but with one important qualification: the density may vary with position! It just doesn't vary along a dynamical path. Energy Gradient and Phase Space VelocityFor a time-independent Hamiltonian, the path in phase space
This vector is perpendicular to the gradient vector, as it must be, of course, since the system moves along a constant energy path. But, interestingly, it has the same magnitude as the gradient vector! What is the significance of that? Imagine a small square sandwiched between two phase space paths close together in energy, and suppose the distance between the two paths is decreasing, so the square is getting squeezed, at a rate equal to the rate of change of the energy gradient. But at the same time it must be getting stretched along the direction of the path, an amount equal to the rate of change of phase space velocity along the path -- and they are equal. So, this is just Liouville again, its area doesn't change. | |
|
| |
| Total comments: 0 | |
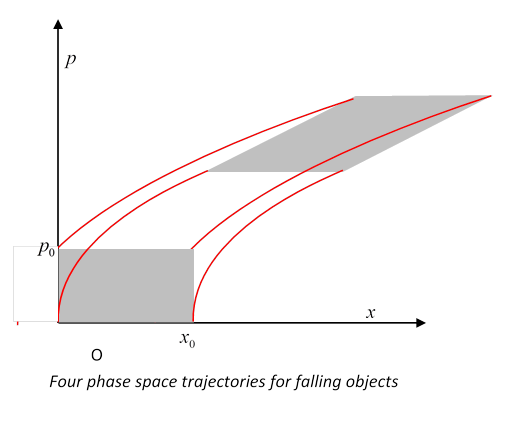 Here's an example from Taylor of paths in phase space: four identical falling bodies are released simultaneously, see figure,
Here's an example from Taylor of paths in phase space: four identical falling bodies are released simultaneously, see figure, 

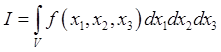
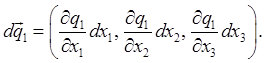
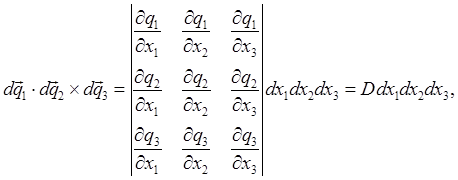
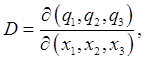

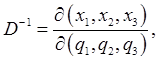


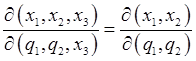 ,
,
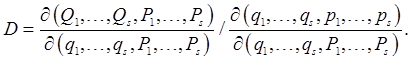
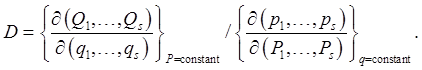
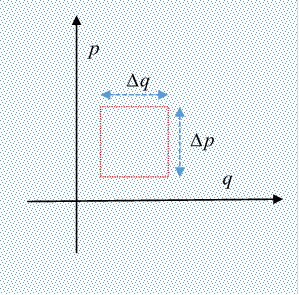 Here we'll take a slightly different point of view: we'll look at a small square in phase space and track how its edges are moving, to prove its volume isn't changing. (We'll stick to one dimension, but the generalization is straightforward.)
Here we'll take a slightly different point of view: we'll look at a small square in phase space and track how its edges are moving, to prove its volume isn't changing. (We'll stick to one dimension, but the generalization is straightforward.)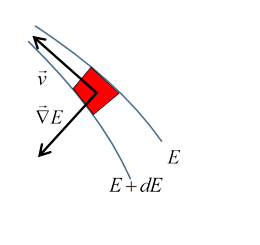 here
here