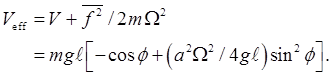Motion in a Rapidly Oscillating Field: the Ponderomotive Force

Michael Fowler

Introduction

Imagine first a particle of massmoving along a line in a smoothly varying potential , so  Now add in a rapidly oscillating force, not necessarily small, acting on the particle:

where  are in general functions of position. This force is oscillating much more rapidly than any oscillation of the particle in the original potential, and we'll assume that the position of the particle as a function of time can be written as a sum of a "slow motion"  and a rapid oscillation ,

We'll also assume that the amplitude of the oscillations, determined by the strength of the force and the frequency, is small compared with distances over which the original fixed potential and the coefficients vary substantially.

You might be thinking at this point, well, isn't  just the path the particle would describe in  alone, and the forcejust jiggles it about that path? Surprisingly, the answer is no. For example, a rigid pendulum confined to rotation in a vertical plane, but with its point of support driven in fairly small amplitude rapid up-and-down oscillations from the outside, can be stable pointing upwards. For motion on the slow timescale associated with the original potential, the rapidly oscillating imposed force is equivalent to an effective potential.

This turns out to have important practical consequences. For a charged particle in a rapidly oscillating electric field, the effective potential from the oscillation is proportional to , generating a force driving the particle towards regions of weaker field. It is termed the ponderomotive force.

For plasma physicists, the ponderomotive force has one very important property -- it drives the positive and negative particles in the same direction, and so gives a different tool from the usual electric and magnetic fields for containing a plasma.

In the analysis below, following Landau, we have a fixed potential and a fast oscillating field superimposed. However, we could just have a non-uniform fast oscillating field, with an equation of motion and still write the particle path as a sum of slow moving and jiggling components,  Fast oscillating electric fields (crossed laser beams) are used to trap ultracold ions and atoms, using the ponderomotive force. It has been suggested that atoms trapped in this way could be part of a quantum computer (Turker, arXiv: 1308.0573v1).

Finding the Effective Potential Generated by the Oscillating Force

As stated above, our system is a particle of massmoving in one dimension in a time-independent potential and subject to a rapidly oscillating force

.

The oscillation's strength and frequency are such that the particle only moves a small distance in during one cycle, and the oscillation is much faster than any oscillation possible in the potential alone.

The equation of motion is

The particle will follow a path

where describes rapid oscillations about a smooth path, and the average value of over a period  is zero.

Expanding to first order in,

This equation has smooth terms and rapidly oscillating terms on both sides, and we can equate them separately. The leading oscillating terms are

We've dropped the terms on the right of order but kept  because 

So to leading order in the rapid oscillation,

.

Now, averaging the full equation of motion with respect to time (smoothing out the jiggle, matching the slow-moving terms), the  on the left and the  on the right both disappear (but cancel each other anyway), the  term averages to zero on the assumption that the variation of  over a cycle of the fast oscillation is negligible, but we cannot drop the average

Incorporating this nonzero term, we have an equation of "slow motion"

where, using 

The effective potential is the original plus a term proportional to the kinetic energy of the oscillation.

Stability of a Pendulum with a Rapidly Oscillating Vertical Driving Force

Recall now the Lagrangian for the simple (rigid) pendulum of lengthmassangle from vertically down constrained to move in a vertical plane, point of support driven to oscillate vertically with amplitude  and frequency (from the section on parametric resonance),

.

Our previous analysis of this system was for driving frequencies near double the natural frequency. Now we'll investigate the behavior for driving frequencies far more rapid than the natural frequency.

The equation of motion, 

is

so evidently the external driving force is , (Landau has a misprint -- an extra  in this, p 95) and, from the previous section, (except that for the pendulum we are using not for the external driving frequency)

For small,  and for  the upwardposition is stable!

At first glance, this may seem surprising: the extra term in the potential from the oscillations is like a kinetic energy term for the oscillating movement. Surely the pendulum is oscillating more in the vertically up position than when it's to one side? So why isn't that a maximum of the added effective potential? The point is that the relevant variable is not the pendulum's height above some fixed point, the variable is  -- and the rapid oscillations of  are minimum (zero) in the vertically up position.

Hand-Waving Explanation of the Ponderomotive Force

Let's look again at the vertically stable pendulum: the quiver force has sufficient frequency that although the quivering motion is of small amplitude, it drives the pendulum to the vertical position. To see what's going on, we'll replace the oscillating force with a series of discrete impulses of alternating sign. Remember, the impulse on the pendulum will be in a vertical direction, but the pendulum is constrained to move along the circular arc. Therefore, the impulse it feels is the component along this path. If it is away from the vertical, the greater its deviation the greater the effective impulse, so as it quivers back and forth it feels greater drive pushing it back up towards the vertical, since it feels that impulse when it's further down. If it does feel a downward impulse at its low point, that will set it up for a greater upward impulse as it goes down.

This can also be understood for a charged particle in an oscillating electromagnetic field in terms of radiation pressure. Where the oscillating field is more intense, there is more radiation pressure, so the particle will be driven by the pressure imbalance towards the regions where the field is weakest.

Pendulum with Top Point Oscillating Rapidly in a Horizontal Direction

Take the coordinates of to be  The Lagrangian, omitting the term depending only on time, and performing an integration by parts and dropping the total derivative term, (following the details of the analysis above for the vertically driven pendulum) is

It follows that (the only difference infrom the vertically driven point of support is the final  instead of ) and

If  is stable. If  the stable position is 

That is, at high frequency, the rest position is at an angle to the vertical! In this case, the ponderomotive force towards the direction of least angular quiver (in this case the horizontal direction) is balanced by the gravitational force.