1:10 AM Maupertuis' Principle: Minimum Action Path at Fixed Energy | |
Maupertuis' Principle: Minimum Action Path at Fixed EnergyDivine GuidanceIncredibly, Maupertuis came up with a kind of principle of least action in 1747, long before the work of Lagrange and Hamilton. Maupertuis thought a body moved along a path such that the sum of products of mass, speed and displacement taken over time was minimized, and he saw that as the hand of God at work. This didn't go over well with his skeptical fellow countrymen, such as Voltaire, and in fact his formulation wasn't quite right, but history has given him partial credit, his name on a least action principle. Suppose we are considering the motion of a particle moving around in a plane from some initial point and time It's Not About TimeBut that's not what you're interested in doing! Of course you want the ball to get in the hole, but you're not obsessed with how long it takes to get there. Yet without that time requirement, there are obviously many possible paths. If you hit it really fast, so its kinetic energy is far greater than the gravitational potential energy variations in the bumpy green, it will go close to a straight line (we're assuming that when it gets over the hole, it will drop in). As you slow down, the winning path will deviate from a straight line because of the uneven terrain. So the physical path to the hole will vary continuously with initial kinetic energy. Maupertuis' principle is about what is the path So now we're fixing the beginning and end points in space, but allowing possible variation in the final time. Also, we're fixing the energy: From the expression for the differential of action in terms of varying the endpoint (as well as the rest of the path -- remember, that gives the integral term that disappears along the dynamical path), we have all
(Since we're restricting to paths with energy The Abbreviated ActionWriting the action in the integral form along this constant energy path, we can trivially do the time integral:
Therefore, from the result
The abbreviated action for the physical path is the minimum among all paths satisfying energy conservation with total energy Naturally, since this is a path through configuration space, to evaluate the abbreviated action
it must be expressed in terms of the
we find the abbreviated action
This is indeed an integral along a path in configuration space, but we need to get rid of the That is, (following Landau)
from which
(This doesn't look like a very healthy mathematical object, but as you'll see, it's fine.) Hence
To take a very simple case; if there is no potential, and just a free particle, If we have a particle of mass
where The matrix Exercise: use Maupertuis' principle to find the path of a cannonball, energy Maupertuis' Principle and the Time-Independent Schrodinger EquationRecall that the action, multiplied by | |
|
| |
| Total comments: 0 | |
 ,
,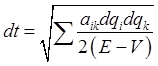 .
.