The Hamilton-Jacobi Equation
Michael Fowler
Back to Configuration Space
We've established that the action, regarded as a function of its coordinate endpoints and time, satisfies
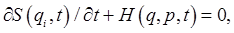
and at the same time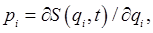 
so 
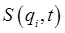obeys the first-order differential equation
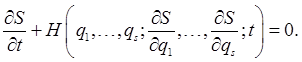
This is the Hamilton-Jacobi equation.
Notice that we're now back in configuration space!
For example, the Hamilton-Jacobi equation for the simple harmonic oscillator in one dimension is
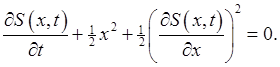
(Notice that this has some resemblance to the Schrödinger equation for the same system.)
If the Hamiltonian has no explicit time dependence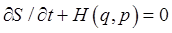 
becomes just ![]()
...
Read more »
and substituting the 
in that equation from the planar equation
where
is the vector perpendicular to the plane from the origin to the plane, gives a quadratic equation in 
This translates into a quadratic equation in the plane -- take the line of intersection of the cutting plane with the 
Imagine a particle in one dimension oscillating back and forth in some potential. The potential doesn't have to be harmonic, but it must be such as to trap the particle, which is executing periodic motion with period
. Now suppose we gradually change the potential, but keeping the particle trapped. That is, the potential depends on some parameter
, which we change gradually, meaning over a time much greater than the time of oscillation: 