« 1 2 ... 4 5 6 7 8 ... 29 30 »
Mechanical Similarity and the Virial Theorem
Some Examples
Similar triangles are just scaled up (or down) versions of each other, meaning they have the same angles. Scaling means the same thing in a mechanical system: if a planet can go around the sun in a given elliptical orbit, another planet can go in a scaled up version of that ellipse (the sun remaining at the focus). But it will take longer: so we can't just scale the spatial dimensions, to get the same equation of motion we must scale time as well, and not in general by the same factor.
In fact, we can establish the relative scaling of space and time in this instance with very simple dimensional analysis. We know the planet's radial acceleration goes as the inverse square of the distance, so (radial acceleration)x(distance)2 = constant, the dimensionality of this expression is  , so  , the square of the time of one orbit is proportional to the cube of the size of the orbit. A little more explicitly, the acceleration  so for the same 
...
Read more »
|
Hamilton's Principle and Noether's Theorem
Introduction: Galileo and Newton
In the discussion of calculus of variations, we anticipated some basic dynamics, using the potential energy  for an element of the catenary, and conservation of energy  for motion along the brachistochrone. Of course, we haven't actually covered those things yet, but you're already very familiar with them from your undergraduate courses, and my aim was to give easily understood physical realizations of minimization problems, and to show how to find the minimal shapes using the calculus of variations.
At this point, we'll begin a full study of dynamics, starting with the laws of motion. The text, Landau, begins (page 2!) by stating that the laws come from the principle of least action, Hamilton's principle. This is certainly one possible approach, but confronted with it for the first time, one might well wonder where it came from. I prefer a gentler introduction, more or less following the historical order: Galileo, then Newton, then Lagrange and his colleagues, then Hamilton. The two approaches are of course equivalent. Naturally, you've seen most of this earlier stuff before, so here is a very brief s
...
Read more »
|
Fermat's Principle of Least Time
9/1/15
Another Minimization Problem
Here's another minimization problem from the 1600's, even earlier than the brachistochrone. Fermat famously stated in the 1630's that a ray of light going from point A to point B always takes the route of least time -- OK, it's trivially true in a single medium, light rays go in a straight line, but it's a lot less obvious if, say, A is in air and B in glass. Notice that this is closely related to our previous topic, the calculus of variations -- if this is a minimal time path, varying the path by a small amount will not change the time taken to first order. (Historical note: actually what amounted to Fermat's principle was first stated by Alhazen, in Baghdad, around 1000 AD.)
This seemed very mysterious when first extensively discussed, in the 1600's. In the last part of that century, and through the 1700's, Newton was the dominant figure, and he believed that light was a stream of particles. But how could the particle figure out the shortest time path from A to B?
In fact, there was one prominent physicist, Huygens, who thought light might be a wave. The main objection to this idea was that waves go around corners, at least to some extent, it seemed that light didn't. (Also, they exhibit diffraction effects, which no one thought they'd seen for light, although in fact Newton himself had observed diffrac
...
Read more »
|
The Calculus of Variations
Introduction
We've seen how Whewell solved the problem of the equilibrium shape of chain hanging between two places, by finding how the forces on a length of chain, the tension at the two ends and its weight, balanced. We're now going to look at a completely different approach: the equilibrium configuration is an energy minimum, so small deviations from it can only make second-order changes in the gravitational potential energy. Here we'll find how analyzing that leads to a differential equation for the curve, and how the technique developed can be successfully applied of a vast array of problems.
The Catenary and the Soap Film
The catenary is the curved configuration  of a uniform inextensible rope with two fixed endpoints at rest in a constant gravitational field. That is to say, it is the curve that minimizes the gravitational potential energy
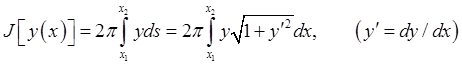
where we have taken the rope density and  both equal to unity for mathematical convenience. Usual
...
Read more »
|
|
degrees of freedom, the spatial configuration at some instant of time is completely specified by a set of
's. The 
.
and