1. Introductory Lecture on Statics: the Catenary and the Arch

What? Statics?

Why begin a course on classical dynamics with a statics example? The reason is that the most important underlying principle of classical dynamics, and much of the rest of physics, is Hamilton’s Principle of Least Action: a system’s time development can always be describes as a path through some multidimensional parameter space (positions, velocities of all its component parts) and the path it actually follows is the one that (on varying the path) minimizes the integral of a certain function, called the action, along that path. A generalization of this principle by Dirac and Feynman (the "sum over paths") led to a fruitful reformulation of quantum mechanics and quantum field theory, now widely used.

The mathematical machinery necessary to minimize an integral along a path by varying the path is called the calculus of variations, so that’s what we have to master. To see how it works, we’ll first apply it to a simple example: finding the curve describing a uniform rope hanging between two points under gravity. The “action” for this statics problem is of course just the potential energy. And, to be sure we’ve found the right answer, we’ll first solve the problem by more traditional statics techniques. So this is where we begin.

The Catenary

What is the ... Read more »

Analyzing Waves on a String

Michael Fowler 5/30/08

From Newton’s Laws to the Wave Equation

Everything there is to know about waves on a uniform string can be found by applying Newton’s Second Law, 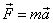, to one tiny bit of the string.  Well, at least this is true of the small amplitude waves we shall be studying—we’ll be assuming the deviation of the string from its rest position is small compared with the wavelength of the waves being studied.  This makes the math simpler, and is an excellent approximation for musical instruments, etc.   Having said that, we’ll draw diagrams, like the one below, with rather large amplitude waves, to show more clearly what’s going on.

 

 

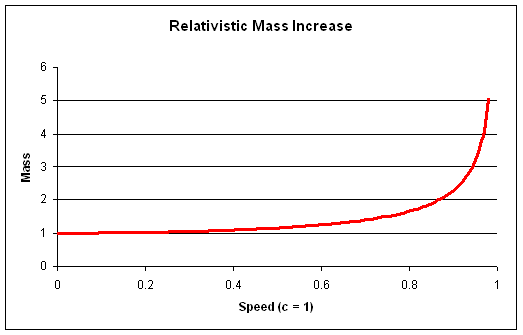
Let’s write down 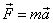 for the small length of string between x and x + Dx in the diagram above. 

 

Taking the st ... Read more »

Remarks on General Relativity

Michael Fowler 
University of Virginia

Einstein’s Parable

In Einstein’s little book Relativity: the Special and the General Theory, he introduces general relativity with a parable.  He imagines going into deep space, far away from gravitational fields, where any body moving at steady speed in a straight line will continue in that state for a very long time.  He imagines building a space station out there - in his words, “a spacious chest resembling a ... Read more »

Transforming Energy into Mass: Particle Creation

Michael Fowler, University of Virginia

Pion Production

We have mentioned how, using a synchrocyclotron, it is possible to accelerate protons to relativistic speeds.  The rest energy of a proton m_pc² is 938 MeV, using here the standard high energy physics energy unit: 1 MeV = 10⁶ eV.  The neutron is a bit heavier—m_nc² = 940 MeV.  (The electron is 0.51 MeV).  Thus to accelerate a proton to relativistic speeds implies giving it a K.E. of order 1,000 MeV, or 1 GeV. 

The standard operating procedure of high energy physicists is to accelerate particles to relativistic speeds, then smash them into other particles to see what happens.  For example, fast protons will be aimed at protons at rest (hydrogen atoms, in other words—the electron can be neglected).  These proton-proton collisions take place inside some kind of detection apparatus, so the results can be observed.  One widely-used detector is the bubble chamber: a transparent container filled with a superheated liquid.  The electric field of a rapidly moving charged particle passing close to a molecule can dislodge an electron, so an energetic particle moving through the liquid leaves a trail of ionized molecules. These give centers about which bubbles can n ... Read more »

Energy and Momentum in Lorentz Transformations

Michael Fowler, University of Virginia

How Does the Total Energy of a Particle Depend on Speed?

We have a formula for the total energy E = K.E. + rest energy,

so we can see how total energy varies with speed.

The momentum varies with speed as

.

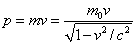How Does the Total Energy of a Particle Depend on Momentum?

It turns out to be useful to have a formula for E in terms of p.

Now

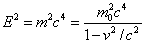
so

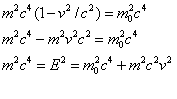
hence using p = mv we find

_{... Read more »}